Predicting Gel Propagation Through Fractures
Our new model can be applied to predict propagation of formed gels through fractures. The rate of gel front propagation, dL/dt, in a fracture can be found from a mass balance.
In Eq. 1, hf is fracture height, wf is fracture width, qt is total volumetric injection rate, and ul is water leakoff rate. Combined with our new model for water leakoff from gels in fractures (Eq. 2), Eq. 1 can be solved numerically to predict rates of gel front propagation and gel dehydration.
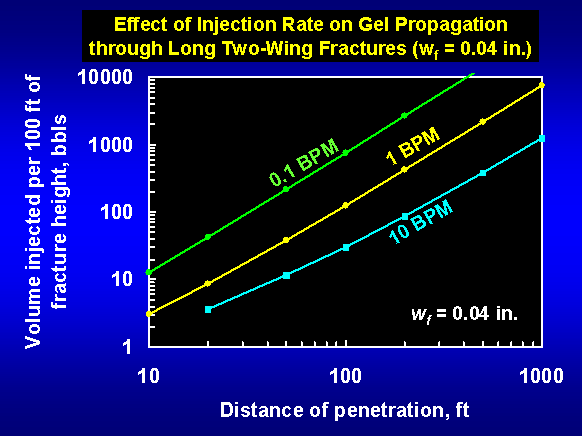
The figure above presents these predictions for three injection rates (0.1 to 10 barrels per minute, BPM) in 0.04-in.-wide, two-wing fractures using our standard Cr(III)-acetate-HPAM gel [1-day old 0.5% Alcoflood 935 crosslinked with 0.0417% Cr(III) acetate at 41°C]. At a given rate, the figure shows the gel volume that must be injected to achieve a given distance of penetration along the fracture. This volume increased with distance of penetration raised approximately to the 1.5 power. For a given distance of penetration, the required gel volume decreased substantially with increased injection rate. For example, to penetrate 200 ft, the required gel volume was 5 times less at 10 BPM than at 1 BPM. Therefore, to maximize gel penetration, the highest practical injection rate should be used.
The figure below plots the predicted distances of gel penetration versus the volume of gel injected for three fracture widths during gel injection at 1 barrel per minute. Interestingly, the curves came together at high distances of penetration and low fracture widths. This result occurred because the rate of gel propagation was governed increasingly by the rate of gel dehydration as fracture width decreased or as the desired distance of gel penetration increased. In contrast, for a fixed injection rate, gel propagation was governed simply by the fracture width (or volume) for large fracture widths or small distances of gel penetration.
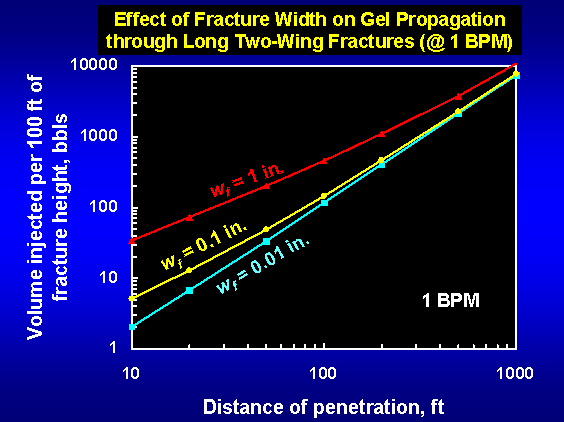
A useful rule of thumb can be realized from the 1.5-power dependence of volume on distance of penetration in the above figures (i.e., at moderate to large distances of penetration). Specifically, if the volume of gel needed to reach a certain distance of penetration is known, then reaching twice that distance requires injecting roughly three times the gel volume. In contrast, for “normal” behavior (i.e., if dehydration did not occur), doubling the distance of penetration only requires a doubling of gel volume. This “normal” behavior is approached for small distances of penetration and wide fractures. For example, the 1-in.-wide fracture approaches normal behavior for small distances of penetration (i.e., the slope approaches 1).